Mixed Integer Programming for optimal risk mitigation strategy
Mixed Integer Programming for optimal risk mitigation strategy
Risk assessment
The Society for Risk Analysis (SRA) defines risk as to the possibility of an unfortunate occurrence, and quantitatively it can be defined as the combination of probability and magnitude/severity of consequences. From this basic definition, we can formalize the risk:
Risk = Probability × Consequence
Another variation that decomposes the probability into two components Threat and Vulnerability:
Risk = Threat × Vulnerability × Consequence
The Threat is the probability of an event occurring and the Vulnerability is uncertainty about and severity of the consequences, given the occurrence of a risk source.
A toy example of risks in a fictional organization :
| Risk | Probability | Severity | Probability × Consequence |
|---|---|---|---|
| Cyberattacks | 0.6 | 900 | 540 |
| Talent Retention | 0.7 | 800 | 560 |
| IT Implementation | 0.1 | 350 | 35 |
| Cyber Fraud | 0.3 | 600 | 180 |
| Organizational Change | 0.6 | 400 | 240 |
| Compliance Risk | 0.2 | 200 | 40 |
Suppose for the sake of example, that we have identified the measures that may mitigate all the risks identified above.
| Risk | Risk value before mitigation | Risk value after mitigation | Cost of mitigation measure |
|---|---|---|---|
| Cyberattacks | 540 | 120 | 90 |
| Talent Retention | 560 | 400 | 80 |
| IT Implementation | 35 | 31 | 30 |
| Cyber Fraud | 180 | 45 | 45 |
| Organizational Change | 40 | 36 | 4 |
| Compliance Risk | 240 | 30 | 50 |
Each mitigation measure has a cost, if we have a certain budget of x$ what is the optimal way to allocate which risk to mitigate?
Implementing a prescriptive model of decision making?
If we have an unlimited budget we could afford to mitigate all of the above risks by implementing the mitigation measures. But in the case of a limited budget, a decision should be made about which risk to mitigate.
| Risk value before mitigation | Risk value after mitigation | Reduced risk (ri) | Cost | Decision |
|---|---|---|---|---|
| 540 | 120 | 420 | 90 | d1 |
| 560 | 400 | 160 | 80 | d2 |
| 35 | 31 | 4 | 30 | d3 |
| 180 | 45 | 135 | 45 | d4 |
| 40 | 36 | 4 | 4 | d5 |
| 240 | 30 | 210 | 50 | d6 |
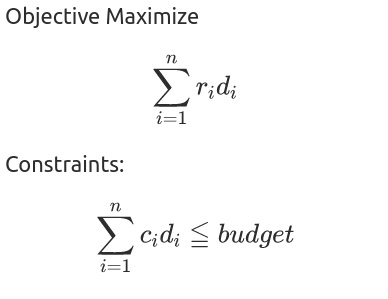
The unknown variables in the above-stated problem are discrete variables, they are integer and restricted to 0 and 1. This is a discrete optimization problem, and since there is no quadratic term it is a linear problem.
This particular resource allocation problem where the decision-makers have to choose from a set of items under a fixed budget is called the knapsack problem. It has been studied extensively from as early as 1897. And because one can choose only an item to be included or not it is usually called the 0–1 knapsack problem. Many algorithms and heuristics exist for solving this type of problem, we choose to use a MIP approach
because it is very flexible when we want to add other constraints and logical considerations.
It should be noted that this problem is NP-complete, thus there is no known algorithm both correct and fast (polynomial-time) that can solve every case of the knapsack problem.
Modeling dependencies
Suppose that a mitigation measure is a dependant on another. For instance, suppose that the implementation of a particular measure d1 cannot be done until the realization of another measure d5. One can include this consideration in the previous model by adding a new constraint.
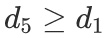
In this case, if we have d1 = 1 then d5 >= 1.
Modeling incompatible decisions
One can further enrich the model by adding more logical considerations, suppose that two mitigation plans are incompatible, they can’t be implemented at the same time. Let’s say d1 and d4 are conflicting mitigation measures, we can choose either d1 or d4:
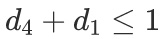
We can consider also three or more conflicting decisions, if d1, d2, and d4 are incompatible and we can choose only one of them, we can simply add the following constraint:
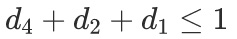
Unfeasible solutions
We can keep adding constraints in order to model complex interaction between the decision, etc. If we have incompatible constraints, it may be possible that there is no solution to the optimization problem.
Mixed Integer Programming with branch-and-Cut
Integer programming is a subset of discreet optimization, that seeks to optimize an objective function subject to constraints. The LP format is a human-friendly modeling format. In practice, though other formats are more adequate for large-scale problems.
The basic constructs are really simple and can be translated directly from the mathematical formulation of the problem. The first section specifies the objective function to optimize and whether it’s a maximization or minimization problem. The second section specifies the constraints, an LP file may contain an arbitrary number of them. Finally, the last section specifies the type of the variable.
Once that the problem was formulated in LP format we can simply feed the file to a MIP optimizer and voilà we have an optimal solution. One such an optimizer is CBC: standing for Coin-or branch and cut, CBC is an open-source mixed-integer linear programming solver written in C++.
For a budget of 150
Maximize
\ The objective function
obj : 420 d1 + 160 d2 + 4 d3 + 135 d4 + 4 d5 + 210 d6
Subject To
c0 : 90 d1 + 80 d2 + 30 d3 + 45 d4 + 4 d5 + 50 d6 <= 150
Binary
d1 d2 d3 d4 d5 d6
End
CBC provides a stand-alone executable that can be called directly from the command line to optimize the problem.

After waiting for some milliseconds the problem was solved.
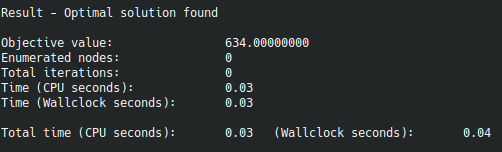
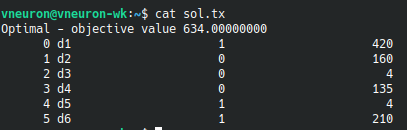
The optimal strategy consists of mitigating risks 1, 5, and 6. This strategy gives a value of 634 for the objective function.
Incorporating more logical constraints (dependencies & conflicting decisions)
- Budget = 150
- d1 cannot be done until the realization of d5.
- d6 and d5 can not be done at the same time.
Maximize*
\ The objective function
obj : 420 d1 + 160 d2 + 4 d3 + 135 d4 + 4 d5 + 210 d6
Subject To
c0 : 90 d1 + 80 d2 + 30 d3 + 45 d4 + 4 d5 + 50 d6 <= 150 c1 : d5 – d1 >= 0
c2 : d6 + d5 <= 1
Binary
d1 d2 d3 d4 d5 d6
End
| Optimal – objective value | Decisions |
|---|---|
| 559 | d1, d4, and d5 |
A cautionary tale

Now that the novice merchant had learned the secrets of Mixed-Integer Programming, he went to apply his newly gained knowledge to optimize which goods to import based on its cost and expected price. He decided to allocate a budget of 1000$ and then he found the optimal solution. An old merchant, seeing what the novice was doing, gave him 1$.
The novice merchant said: “Why you gave me 1$ ?”. The old merchant said: “Redo your calculation with your new budget”. The novice merchant
was enlightened.
Due to the discreet nature of MIP problems, a small variation in the allocated budget can cause a huge difference in the solution.

